先决知识
- 基本的图论和数据结构知识
- 线段树(Segment Tree)
- DFS序(Depth-first-search SEQ.)
基本思想
树链剖分(Tree Chain Partition)的思路是将一整颗树剖分若干条链, 组合这些链成为线性结构从而能使用其他数据结构维护信息.具体地, 按照判链条件来讲有多种剖分方式, 如重链剖分, 长链剖分以及实链剖分. 本文要介绍被广泛运用的重链剖分.
重链剖分以子树的大小为依据来确定该子树的根节点是否在链上, 链的数量不超过 $\log_2N$ 条. 链在树的结构上是延续的, 一条链中的每一个节点所映射到的线性结构上的标号也是延续的. 这样能实现 $\Omicron(\log_2N)$ 级别的任意两点之间的查询树上路径和, 树上路径极值等, 以及对树上单点或区间值的修改操作.
给出定义
- 重子节点(重儿子): 对于一个节点的所有子节点中, 所有子树的节点最多的那一个子节点.
- 轻子节点(轻儿子): 对于一个节点的所有子节点中, 所有不是重子节点的其他子节点.
- 重边: 一条边中如果深度更深的节点是重子节点, 那这条边就叫重边.
- 轻边: 所有不是重边的边.
- 重链: 由一或多条重边连接成的延续的路径.
- 轻链: 所有不是重链的链.
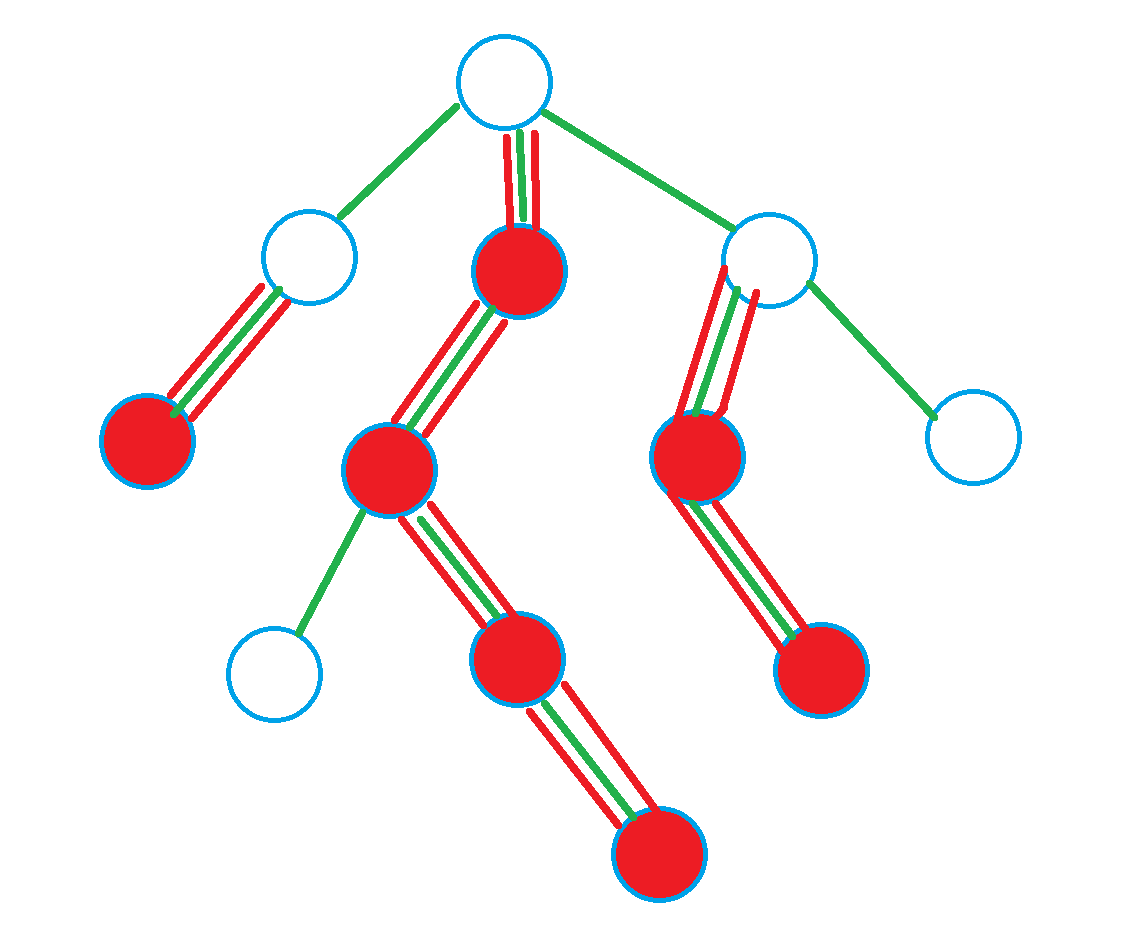
如图, 在这一颗树中, 被以红色填充的点是重子节点, 额外被两条红线标记的边是重边. 该图符合上文给出的定义, 可以看出图上存在三条重链.
过程分析
我们首先通过两次的 $DFS$ 来计算出一些信息.
DFS_1
给出以下伪代码:

这段代码处理了每个节点的 $father, heavy_son, depth, size$ 这些信息, 其中 $size$ 是以这个点为根的子树的点数量.
DFS_2

这段代码处理出每个点映射到线性结构上对应的标号 $index$ 和线性结构每个标号对应到的点 $new_id$. 还按照定义处理出重子节点 $heavy_son$, 以及重链链头信息 $top$.
线段树
随后就能根据 $new_id$ 建出一颗线段树, 提供对区间求和的更新和查询操作. 这是一个很自然的过程, 不多赘述.
路径查询/修改
和常规的倍增 $LCA$ 操作思想类似, 如下:
- 如果两点在同一重链上 (链头相同), 答案加上两点 $index$ 在线段树上的区间和, 结束。
- 否则, 对于深度更深的点, 答案加上链头和当前 $index$ 在线段树上区间和, 跳到所在链头上, 一直如此直到在同一条重链上执行才执行上面的操作.
这里是因为链上连续节点在线性结构上连续的性质. 类似地, 路径修改就是把上面的线段树操作换成区间修改.
子树查询/修改
从前面的$DFS_2$ 可以发现, 重链抛分同样具有 $DFS$ 序的子树连续性质. 所以说只要作一次线段树上的区间查询或者修改操作就行了.
参考实现
LGP3384 模板题
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n, m, r, p, cnt=0,
num[N], hes[N], siz[N], fat[N], dep[N], top[N], idx[N], nid[N];
vector<int> g[N];
int dfs1(int rt, int fa, int deep){
fat[rt]=fa, siz[rt]=1, dep[rt]=deep;
for(auto i : g[rt]){
if(i==fa) continue;
siz[rt]+=dfs1(i, rt, deep+1), hes[rt]=siz[hes[rt]]>siz[i]?hes[rt]:i;
}
return siz[rt];
}
void dfs2(int rt, int tp){
idx[rt]=++cnt, nid[cnt]=num[rt], top[rt]=tp;
if(hes[rt]) dfs2(hes[rt], tp);
for(auto i : g[rt]) if(i!=fat[rt] && i!=hes[rt]) dfs2(i, i);
}
//Start Segment Tree here...
struct Tree{
int sum, laz, len;
}tre[N];
#define l(a) (a<<1)
#define r(a) (a<<1|1)
#define push_up(a) tre[rt].sum = tre[l(rt)].sum+tre[r(rt)].sum
void build_tree(int l, int r, int rt){
tre[rt].len = r-l+1;
if(l==r) { tre[rt].sum=nid[l]; return ;}
int mid = (l+r)>>1;
build_tree(l, mid, l(rt)), build_tree(mid+1, r, r(rt)), push_up(rt);
}
inline void push_down(int rt){
if(!tre[rt].laz) return;
tre[l(rt)].laz+=tre[rt].laz, tre[l(rt)].laz%=p;
tre[r(rt)].laz+=tre[rt].laz, tre[r(rt)].laz%=p;
tre[l(rt)].sum+=tre[rt].laz*tre[l(rt)].len, tre[l(rt)].sum%=p;
tre[r(rt)].sum+=tre[rt].laz*tre[r(rt)].len, tre[r(rt)].sum%=p,
tre[rt].laz=0;
}
void update_tree(int stdl, int stdr, int l, int r, int rt, int val){
if(stdl<=l&&r<=stdr){
tre[rt].sum += tre[rt].len*val%p, tre[rt].sum%=p, tre[rt].laz+=val;
return;
}
push_down(rt);
int mid = (l+r)>>1;
if(stdl<=mid) update_tree(stdl, stdr, l, mid, l(rt), val);
if(mid+1<=stdr) update_tree(stdl, stdr, mid+1, r, r(rt), val);
push_up(rt);
}
int query_tree(int stdl, int stdr, int l, int r, int rt){
if(stdl<=l&&r<=stdr) return tre[rt].sum;
push_down(rt);
int mid = (l+r)>>1, ret=0;
if(stdl<=mid) ret+=query_tree(stdl, stdr, l, mid, l(rt));
if(mid+1<=stdr) ret+=query_tree(stdl, stdr, mid+1, r, r(rt));
return (ret+p)%p;
}
void update_chain(int x, int y, int val){
int tmpx = top[x], tmpy = top[y];
while(tmpx != tmpy){
if(dep[tmpx]<dep[tmpy]) swap(x, y), swap(tmpx, tmpy);
update_tree(idx[tmpx], idx[x], 1, cnt, 1, val);
x = fat[tmpx], tmpx = top[x];
}
if(idx[x] > idx[y]) swap(x, y);
update_tree(idx[x], idx[y], 1 ,cnt, 1, val);
}
int query_chain(int x, int y){
int ret=0, tmpx=top[x], tmpy=top[y];
while(tmpx != tmpy){
if(dep[tmpx]<dep[tmpy]) swap(x, y), swap(tmpx, tmpy);
ret += query_tree(idx[tmpx], idx[x], 1, cnt, 1);
x = fat[tmpx], tmpx = top[x];
}
if(idx[x]>idx[y]) swap(x, y);
return (ret + query_tree(idx[x], idx[y], 1, cnt, 1) + p)%p;
}
int main(){
cin>>n>>m>>r>>p;
for(int i=1;i<=n;i++) cin>>num[i], num[i]%=p;
for(int i=1, x, y;i<n;i++) cin>>x>>y, g[x].push_back(y), g[y].push_back(x);
dfs1(r, -114514, 0), dfs2(r, r), build_tree(1, n, 1);
while(m--){
int opt, x, y, z;
cin>>opt;
if(opt==1) cin>>x>>y>>z, update_chain(x, y, z);
else if(opt==2) cin>>x>>y, cout<<query_chain(x, y)<<'\n';
else if(opt==3) cin>>x>>y, update_tree(idx[x], idx[x]+siz[x]-1, 1, n, 1, y);
else if(opt==4)
cin>>x, cout<<query_tree(idx[x], idx[x]+siz[x]-1, 1, n, 1)<<'\n';
}
}
LGP3178/HAOI2015 “树上操作”
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+5;
int n, m, cnt=0,
num[N], hes[N], siz[N], fat[N], dep[N], top[N], idx[N], nid[N];
vector<int> g[N];
int dfs1(int rt, int fa, int deep){
fat[rt]=fa, siz[rt]=1, dep[rt]=deep;
for(auto i : g[rt]){
if(i==fa) continue;
siz[rt]+=dfs1(i, rt, deep+1), hes[rt]=siz[hes[rt]]>siz[i]?hes[rt]:i;
}
return siz[rt];
}
void dfs2(int rt, int tp){
idx[rt]=++cnt, nid[cnt]=num[rt], top[rt]=tp;
if(hes[rt]) dfs2(hes[rt], tp);
for(auto i : g[rt]) if(i!=fat[rt] && i!=hes[rt]) dfs2(i, i);
}
//Start Segment Tree here...
struct Tree{
int sum, laz, len;
}tre[N];
#define l(a) (a<<1)
#define r(a) (a<<1|1)
#define push_up(a) tre[rt].sum = tre[l(rt)].sum+tre[r(rt)].sum
void build_tree(int l, int r, int rt){
tre[rt].len = r-l+1;
if(l==r) { tre[rt].sum=nid[l]; return ;}
int mid = (l+r)>>1;
build_tree(l, mid, l(rt)), build_tree(mid+1, r, r(rt)), push_up(rt);
}
inline void push_down(int rt){
if(!tre[rt].laz) return;
tre[l(rt)].laz+=tre[rt].laz;
tre[r(rt)].laz+=tre[rt].laz;
tre[l(rt)].sum+=tre[rt].laz*tre[l(rt)].len;
tre[r(rt)].sum+=tre[rt].laz*tre[r(rt)].len,
tre[rt].laz=0;
}
void update_tree(int stdl, int stdr, int l, int r, int rt, int val){
if(stdl<=l&&r<=stdr){
tre[rt].sum += tre[rt].len*val, tre[rt].laz+=val;
return;
}
push_down(rt);
int mid = (l+r)>>1;
if(stdl<=mid) update_tree(stdl, stdr, l, mid, l(rt), val);
if(mid+1<=stdr) update_tree(stdl, stdr, mid+1, r, r(rt), val);
push_up(rt);
}
int query_tree(int stdl, int stdr, int l, int r, int rt){
if(stdl<=l&&r<=stdr) return tre[rt].sum;
push_down(rt);
int mid = (l+r)>>1, ret=0;
if(stdl<=mid) ret+=query_tree(stdl, stdr, l, mid, l(rt));
if(mid+1<=stdr) ret+=query_tree(stdl, stdr, mid+1, r, r(rt));
return (ret);
}
void update_chain(int x, int y, int val){
int tmpx = top[x], tmpy = top[y];
while(tmpx != tmpy){
if(dep[tmpx]<dep[tmpy]) swap(x, y), swap(tmpx, tmpy);
update_tree(idx[tmpx], idx[x], 1, cnt, 1, val);
x = fat[tmpx], tmpx = top[x];
}
if(idx[x] > idx[y]) swap(x, y);
update_tree(idx[x], idx[y], 1 ,cnt, 1, val);
}
int query_chain(int x, int y){
int ret=0, tmpx=top[x], tmpy=top[y];
while(tmpx != tmpy){
if(dep[tmpx]<dep[tmpy]) swap(x, y), swap(tmpx, tmpy);
ret += query_tree(idx[tmpx], idx[x], 1, cnt, 1);
x = fat[tmpx], tmpx = top[x];
}
if(idx[x]>idx[y]) swap(x, y);
return ret + query_tree(idx[x], idx[y], 1, cnt, 1);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>num[i];
for(int i=1, x, y;i<n;i++) cin>>x>>y, g[x].push_back(y), g[y].push_back(x);
dfs1(1, -114514, 0), dfs2(1, 1), build_tree(1, n, 1);
while(m--){
int opt, x, y, z;
cin>>opt;
if(opt==1) cin>>x>>y, update_tree(idx[x], idx[x], 1, n, 1, y);
else if(opt==2) cin>>x>>y, update_tree(idx[x], idx[x]+siz[x]-1, 1, n, 1, y);
else cin>>x, cout<<query_chain(1, x)<<'\n';
}
}